LeetCode 1: Two Sum Solution in Python

The Two Sum problem from LeetCode is a fundamental challenge in computer science, asking for the identification of two numbers in an array that add up to a given target. This post explains the Python solution to the Two Sum problem, providing insights into its implementation and complexity analysis.

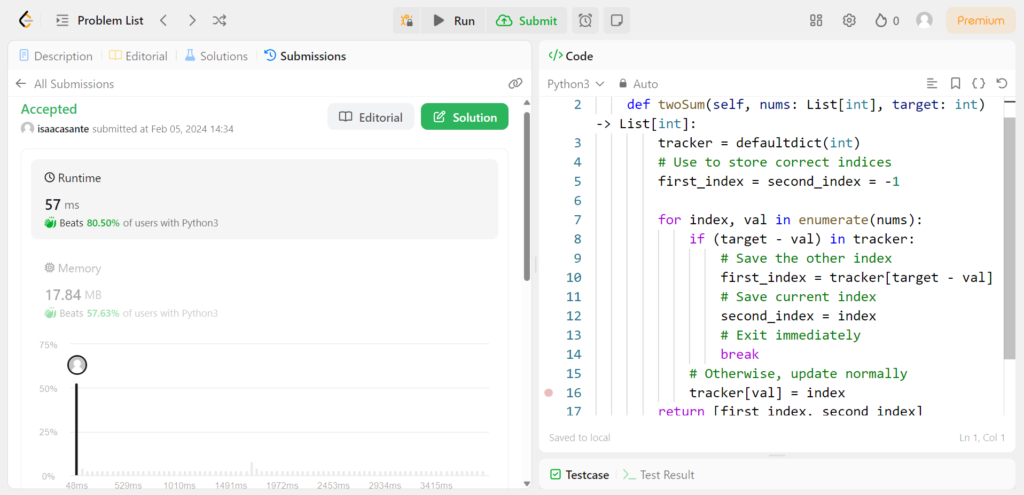
Below is a Python class called Solution, with a method twoSum designed specifically for the Two Sum challenge. Note that this method is provided automatically in the LeetCode code editor when you select Python 3 as the language. In the code snippet below corresponding to my Two Sum Python solution, I have added comments to help read understand the logic.

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        tracker = defaultdict(int)
        # Use to store correct indices
        first_index = second_index = -1 
        
        for index, val in enumerate(nums):
            if (target - val) in tracker:
                # Save the other index
                first_index = tracker[target - val]
                # Save current index
                second_index = index 
                # Exit immediately
                break 
            # Otherwise, update normally
            tracker[val] = index
        return [first_index, second_index]

Understanding the Two Sum Python solution

The twoSum method employs a dictionary named tracker to keep track of the numbers it has encountered and their indices. This strategy allows for efficient checking of whether the complement of the current number (i.e., the difference between the target and the current value) has previously been seen.

As the method iterates over the list nums, it calculates the complement for each value. If this complement exists in tracker, indicating that a pair summing up to the target has been found, the method saves the indices of both the complement (previously stored in tracker) and the current value. This discovery leads to an immediate break from the loop, as the solution has been identified.

If the complement is not found within tracker, the method updates tracker with the current value and its index, allowing the search to continue with the subsequent elements in the list.

Solution Output

The method returns a list containing the indices [first_index, second_index]. These indices represent the positions of the two numbers that sum up to the target. If the method fails to find such a pair, it returns [-1, -1], indicating that no solution exists within the provided list for the Two Sum problem.

Two Sum Time Complexity

The time complexity of this solution is O(n), where n is the number of elements in the list nums. This linear time complexity arises because the method iterates through the list exactly once. Each operation within the loop, including checking for the complement and updating the tracker, is performed in constant time, thanks to the efficient lookup and insertion operations provided by the Python dictionary.

Two Sum Space Complexity

The space complexity of the solution is also O(n). In the worst-case scenario, the tracker dictionary may need to store an entry for nearly every element in nums before finding a solution or determining that no solution exists. Therefore, the amount of memory used by the method grows in proportion to the size of the input list.

This Python solution to the Two Sum problem exemplifies an efficient and straightforward approach to a common algorithmic challenge. By leveraging a hash map to track the indices of elements, the solution achieves linear time and space complexity, making it suitable for large datasets.